TEOREMA DE EUCLIDES

De Euclides (330 a.C al 227 a.C) se sabe muy poco, con certeza, acerca de sus vida. Su gran reputación se debe sin duda a su obra titulada Los Elementos Geométricos, conocida simplemente por Los Elementos.

Además de estas y otras obras, Euclides escribió Los Datos que trata de la resolución de problemas, dándose elementos de la figura y determinándose otros. Los Porismos es una de sus obras perdidas; se cree que trataba de los Lugares Geométricos y de proposiciones sobre transversales. Muchos piensan que esta ha sido la mejor obra de Euclides.

A continuación se presentan dos Teoremas de Euclides, uno referido a un cateto (en un triángulo rectángulo) y otro referido a la altura.

Teorema de Euclides referido a un cateto

“En un triángulo rectángulo la medida de cada cateto es media proporcional geométrica entre las medidas de la hipotenusa y su proyección sobre ella.”

Demostración:

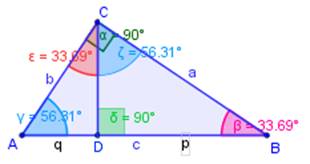Si se tiene un triángulo ABC cualquiera, rectángulo en C, y se proyectan los catetos sobre la hipotenusa, se tiene la siguiente figura (dercha):

donde

DB = p (proyección del cateto a (CB) sobre la hipotenusa)

AD = q (proyección del cateto b (AC) sobre la hipotenusa)

c = p + q

Por semejanza (~) de triángulos, el   ΔACB ~  ΔCDB (son semejantes)

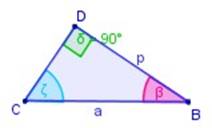Luego;

Que es lo mismo que:

De forma análoga se tiene que ΔACB  ~  ΔADC (a la derecha) ,entonces

Que es lo mismo que:

  

 

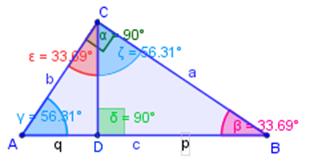
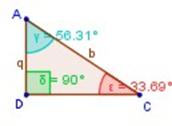
Vistas las fórmulas a las que arribamos utilizando la media proporcional geométrica, podemos enunciar el primer Teorema de Euclides también de la siguiente forma:

“En un triangulo rectángulo, el cuadrado de un cateto es igual al producto de la hipotenusa por la proyección del mismo cateto sobre la hipotenusa”.

Por lo tanto,

  

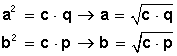
Ejemplos:

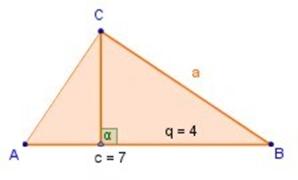1) En la figura a la derecha, determinar a,

si c = 7 y q = 4

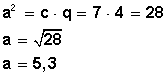
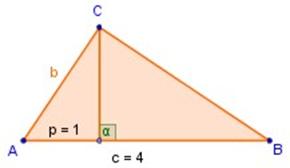2) En la figura a la izquierda, determinar b

si c = 4 y p = 1

 

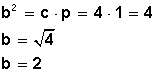
Teorema de Euclides relativo a la altura

“En un triángulo rectángulo la altura correspondiente a la hipotenusa es media proporcional geométrica entre los segmentos que dicha altura determina en ella.”

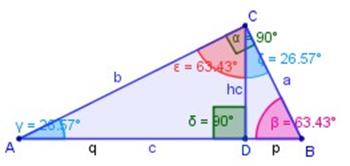Se sabe que ΔADC ~ ΔCDB (semejantes, en la figura a la derecha); por lo tanto, sus lados homólogos (correspondientes) son proporcionales.

Sea hc  (CD) la altura de la hipotenusa (AB = c)

Entonces:

Reemplazando:

Llegamos a: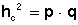 

A partir de esta última fórmula, y tal como en el caso del primer teorema de Euclides, este segundo teorema también se puede expresar de la siguiente manera:

“En un triangulo rectángulo, el cuadrado de la altura de la hipotenusa (hc) es equivalente al producto de las proyecciones de los catetos en la hipotenusa”.

Por lo tanto,  si   h² = p • q    

entonces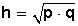             

Ejemplos:

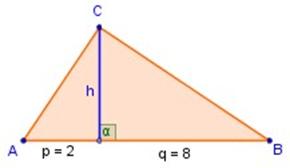1) En la figura a la derecha, determinar h,

si p = 2 y q = 8

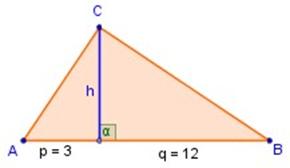2) En la figura a la izquierda, determinar h,

si p = 3 y q = 12

 

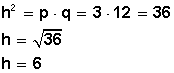
La altura correspondiente a la hipotenusa (hc)de un triángulo también se puede obtener a partir de las medidas de los lados del triángulo, haciendo:

 

ACA LES DEJAMOS UN ENLACE PARA QUE VEAN MEJOR ESTE TEMA
Teorema de Euclides